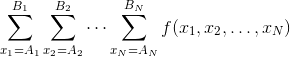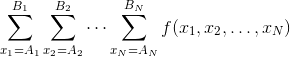配点 : 800 点
問題文
競プロ幼稚園には1~Nの番号がついたN人の子供がいます。えび先生は、区別できないC個のキャンディーを子供たちに分配することにしました。子供iのはしゃぎ度がxiの時、キャンディーをa個もらうと子供iのうれしさはxiaになります。幼稚園の活発度はN人の子供たちのうれしさの積になります。各子供にキャンディーを非負整数個配ってC個配りきる方法それぞれに対して幼稚園の活発度を計算して、その総和を子供たちのはしゃぎ度x1,..,xNの関数とみてf(x1,..,xN)とおきます。Ai,Bi(1≤i≤N)が与えられるので、 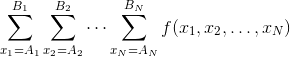
を109+7で割ったあまりを求めてください。
制約
- 1≤N≤400
- 1≤C≤400
- 1≤Ai≤Bi≤400(1≤i≤N)
部分点
- Ai=Bi(1≤i≤N) を満たすデータセットに正解した場合は、部分点として400 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N C
A1 A2 ... AN
B1 B2 ... BN
出力
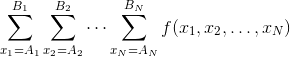
の値を109+7で割ったあまりを出力せよ。
2 3
1 1
1 1
4
Ai=Biなので部分点の条件を満たします。
子供1,2のはしゃぎ度が共に1のもの(f(1,1))を考えればよく、この時、
- 子供1に0個,子供2に3個のキャンディーをあげると、幼稚園の活発度は10∗13=1
- 子供1に1個,子供2に2個のキャンディーをあげると、幼稚園の活発度は11∗12=1
- 子供1に2個,子供2に1個のキャンディーをあげると、幼稚園の活発度は12∗11=1
- 子供1に3個,子供2に0個のキャンディーをあげると、幼稚園の活発度は13∗10=1
従ってf(1,1)=1+1+1+1=4となり、fを足し合わせた答えは4です。
1 2
1
3
14
子供が一人なので、子供1のうれしさが幼稚園の活発度になります。また、キャンディの配り方は2つとも子供1にあげる1通りしかないため、この時の幼稚園の活発度はfの値に等しくなります。
- 子供1のはしゃぎ度が1の時、f(1)=12=1
- 子供1のはしゃぎ度が2の時、f(2)=22=4
- 子供1のはしゃぎ度が3の時、f(3)=32=9
従って答えは1+4+9=14となります。
2 3
1 1
2 2
66
f(1,1)=4,f(1,2)=15,f(2,1)=15,f(2,2)=32 となることがわかるので、答えは4+15+15+32=66になります。
4 8
3 1 4 1
3 1 4 1
421749
部分点の条件を満たします。
3 100
7 6 5
9 9 9
139123417